test đề
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
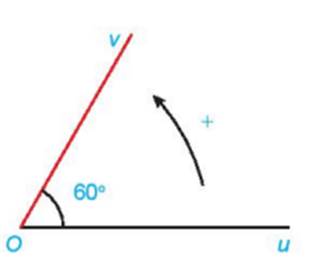
Câu 1: Cho góc hình học 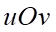 có số đo
có số đo  như hình bên. Số đo của góc lượng giác
như hình bên. Số đo của góc lượng giác 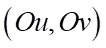 là:
là:
A. sđ 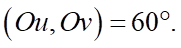 B. sđ
B. sđ 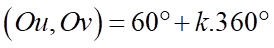
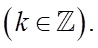
C. sđ 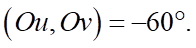 D. sđ
D. sđ 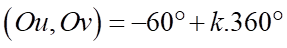
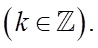
Lời giải
Chọn B
Câu 2: Mệnh đề nào sau đây sai?
A. 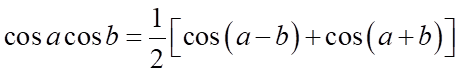 .
.
B. 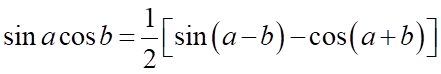 .
.
C. 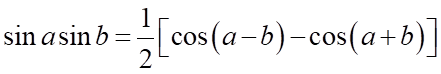 .
.
D. 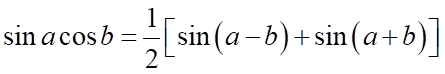 .
.
Lời giải
Chọn B
Ta có 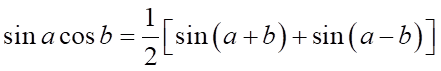 .
.
Câu 3: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. 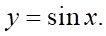 B.
B. 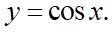 C.
C. 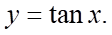 D.
D. 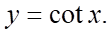
Lời giải
Chọn B
+ Hàm số  là hàm số lẻ.
là hàm số lẻ.
+ Hàm số 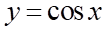 là hàm số chẵn.
là hàm số chẵn.
+ Hàm số 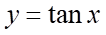 là hàm số lẻ.
là hàm số lẻ.
+ Hàm số 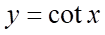 là hàm số lẻ.
là hàm số lẻ.
Vậy B là đáp án đúng.
Câu 4: Cho dãy số 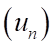 với
với 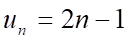 . Năm số hạng đầu tiên của dãy số là
. Năm số hạng đầu tiên của dãy số là
A. 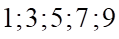 . B.
. B. 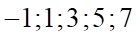 . C.
. C. 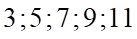 . D.
. D. 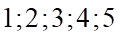 .
.
Lời giải
Chọn A
Ta có: 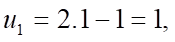
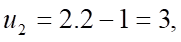
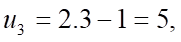
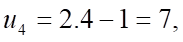
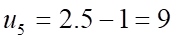 .
.
Câu 5: Cho dãy số 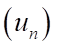 là một cấp số cộng, biết
là một cấp số cộng, biết 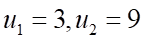 . Công sai
. Công sai 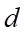 của cấp số cộng này bằng
của cấp số cộng này bằng
A. 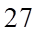 . B.
. B. 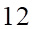 . C.
. C. 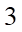 . D.
. D. 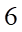 .
.
Lời giải
Chọn D

Câu 6: Cho cấp số nhân 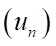 với
với 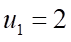 và công bội
và công bội 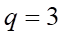 . Tìm số hạng thứ
. Tìm số hạng thứ 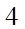 của cấp số nhân?
của cấp số nhân?
A. 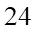 . B.
. B. 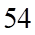 . C.
. C. 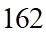 . D.
. D. 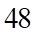 .
.
Lời giải
Chọn B
Có 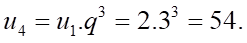
Câu 7: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa mốt của mẫu số liệu trên là
A. 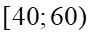 . B.
. B. 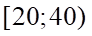 . C.
. C. 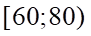 . D.
. D. 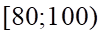 .
.
Lời giải
Chọn A
Mốt 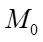 chứa trong nhóm
chứa trong nhóm 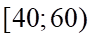
Câu 8: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau:

Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. 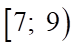 . B.
. B. 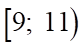 . C.
. C. 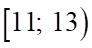 . D.
. D. 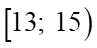 .
.
Lời giải
Chọn B
Goi 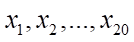 là doanh thu bán hàng trong 20 ngày xếp theo thứ tự không giảm.
là doanh thu bán hàng trong 20 ngày xếp theo thứ tự không giảm.
Khi đó: 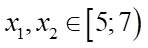 ,
, 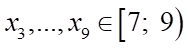 ,,
,, 
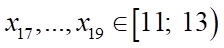 ,
, 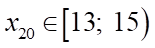
Do đó, trung vị của mẫu số liệu thuộc nhóm 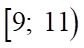
Câu 9: Một hình chóp có đáy là ngũ giác có số cạnh là
A. 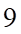 cạnh. B.
cạnh. B. 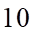 cạnh. C.
cạnh. C. 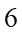 cạnh. D.
cạnh. D. 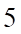 cạnh.
cạnh.
Lời giải
Chọn B
Hình chóp có số cạnh bên bằng số cạnh đáy nên số cạnh của hình chóp là: 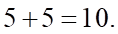
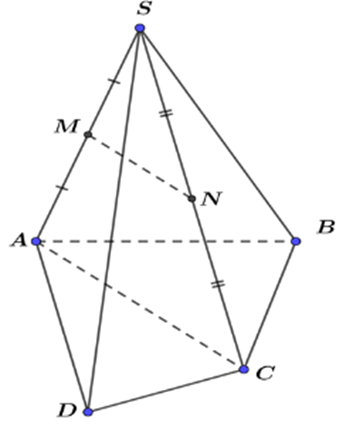
Câu 10: Cho hình chóp tứ giác 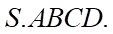 Gọi
Gọi 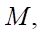
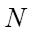 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và  . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A.  . B.
. B.  . C.
. C. 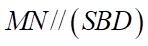 . D.
. D. 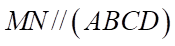
Lời giải
Chọn D
Vì 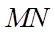 là đường trung bình của tam giác
là đường trung bình của tam giác 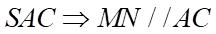 .
.
Mặt khác 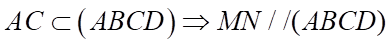 .
.
A. 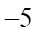 . B.
. B. 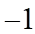 . C.
. C. 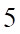 . D.
. D.  .
.
Lời giải
Chọn A
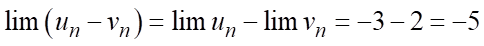 .
.
Câu 12: Giá trị của 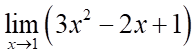 bằng:
bằng:
A. 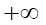 . B.
. B. 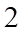 . C.
. C. 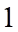 . D.
. D. 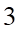 .
.
Lời giải
Chọn B
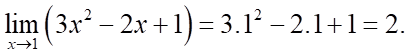
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho 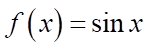 và
và 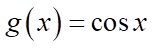 . Các mệnh đề sau đúng hay sai?
. Các mệnh đề sau đúng hay sai?
a) 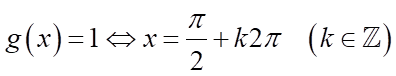
b) 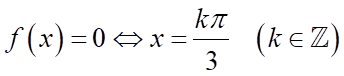
c) 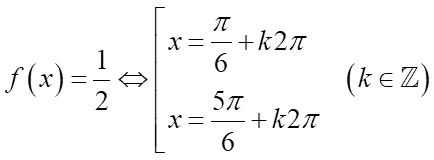
d) Khi phương trình 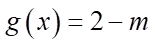 có nghiệm thì giá trị nhỏ nhất của
có nghiệm thì giá trị nhỏ nhất của 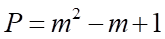 bằng
bằng 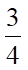 .
.
Lời giải
a) Ta có: 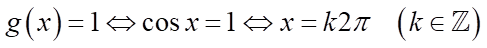 . Suy ra mệnh đề sai.
. Suy ra mệnh đề sai.
b) Ta có: 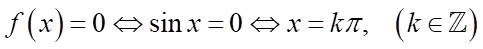 . Suy ra mệnh đề sai
. Suy ra mệnh đề sai
c) Ta có: 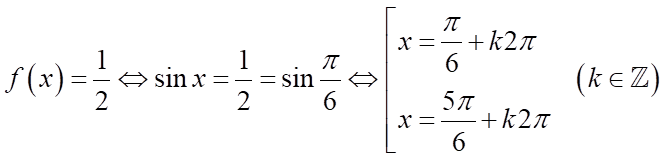 . Suy ra mệnh đề đúng.
. Suy ra mệnh đề đúng.
d) Ta có 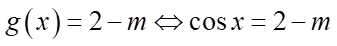 .
.
Phương trình có nghiệm khi 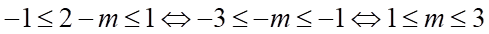
Ta có 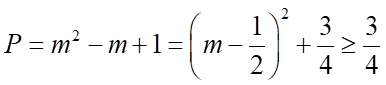
Dấu “=” xảy ra khi 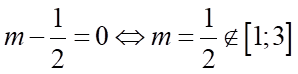
Vậy trên 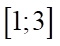 ,
, 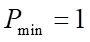 khi
khi 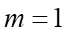 .
.
Suy ra mệnh đề sai.
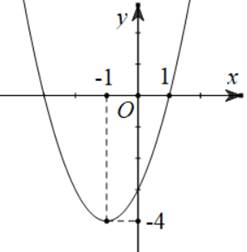
Câu 2: Cho hàm số bậc hai 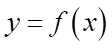 có đồ thị như hình vẽ bên dưới.
có đồ thị như hình vẽ bên dưới.
a) Hàm số đã cho liên tục trên 
b) 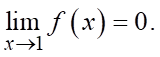
c) 
d) 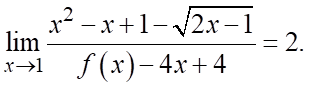
Lời giải
a) Đúng. Hàm số đã cho làm hàm đa thức bậc hai nên hàm số liên tục trên 
b) Đúng. Từ đồ thị, ta có 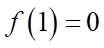 , mà hàm số liên tục tại
, mà hàm số liên tục tại  . Suy ra
. Suy ra 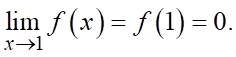
c) Sai. Đặt 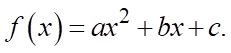
Đồ thị hàm số đã cho có đỉnh 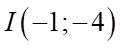 và đi qua
và đi qua 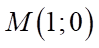 nên
nên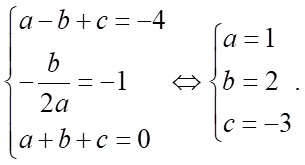
Khi đó 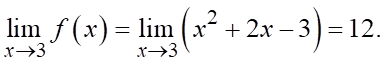
d) Đúng. 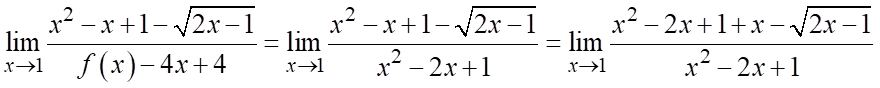
Câu 3: Cho hai vuông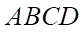 và
và  ở trong hai mặt phẳng phân biệt. Trên các đường chéo
ở trong hai mặt phẳng phân biệt. Trên các đường chéo 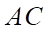 và
và 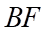 lần lượt lấy các điểm
lần lượt lấy các điểm 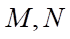 sao cho
sao cho 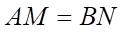 . Các đường thẳng song song với
. Các đường thẳng song song với 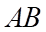 vẽ từ
vẽ từ 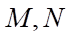 lần lượt cắt
lần lượt cắt 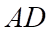 và
và 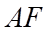 tại
tại 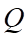 và
và 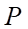 .
.
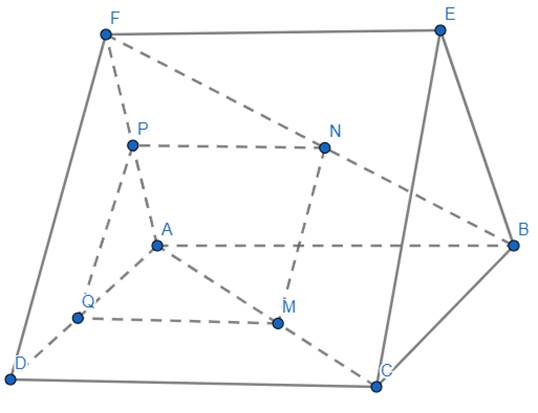
a)  .
.
b) 4 điểm 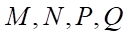 đồng phẳng.
đồng phẳng.
c) 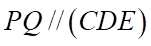 .
.
d) 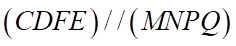 .
.
Lời giải
a) Đúng. Ta có 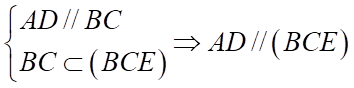 .
.
Tương tự 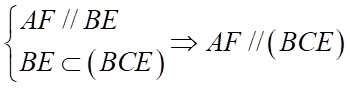 .
.
Mà 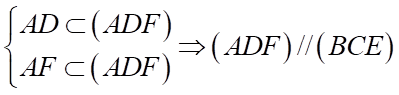 . Suy ra a) Đúng.
. Suy ra a) Đúng.
b) Đúng. Ta có: 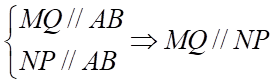 suy ra 4 điểm
suy ra 4 điểm đồng phẳng Suy ra b) Đúng.
đồng phẳng Suy ra b) Đúng.
c) Đúng. Vì  và
và 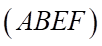 là các hình vuông nên
là các hình vuông nên 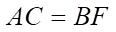 .
.
Ta có 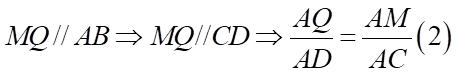 .
.
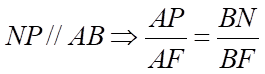 .
.
Theo giả thiết 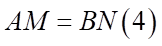 .
.
Từ, ta được 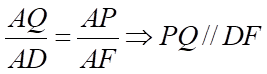
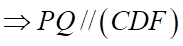 .
.
Ta có: 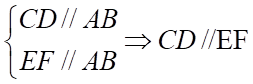 suy ra 4 điểm
suy ra 4 điểm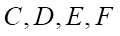 đồng phẳng
đồng phẳng 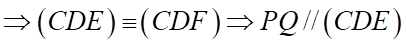
Suy ra c) Đúng
d) Đúng. Ta có: 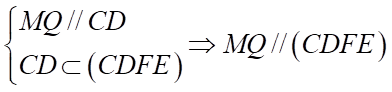 .
.
Mà 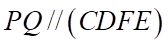 ).
).
Như vậy ta có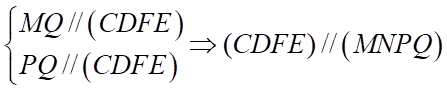 . Suy ra d) Đúng
. Suy ra d) Đúng
Câu 4: Cho hình chóp 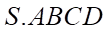 , có đáy
, có đáy 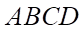 là một hình bình hành tâm
là một hình bình hành tâm 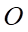 . Gọi
. Gọi 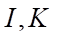 lần lượt là trung điểm của
lần lượt là trung điểm của 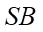 và
và 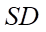 . Khi đó:
. Khi đó:
a) 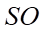 là giao tuyến của
là giao tuyến của 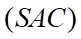 và
và 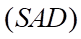 .
.
b) Giao tuyến của 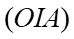 và
và 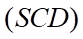 là đường thẳng đi qua
là đường thẳng đi qua 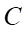 và song song với
và song song với 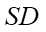 .
.
c) Giao điểm 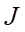 của
của 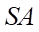 với
với 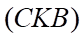 thuộc đường thẳng đi qua
thuộc đường thẳng đi qua 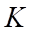 và song song với
và song song với 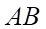 .
.
d) 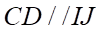 .
.
Lời giải
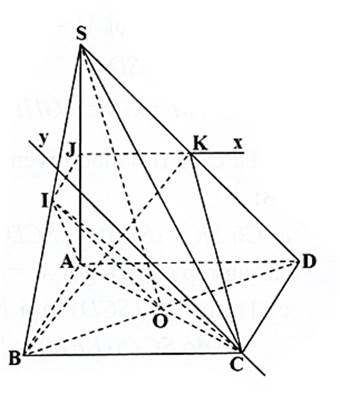
a) Sai. 
b) Đúng. Có  là đường trung bình của
là đường trung bình của  .
.
Ta có: 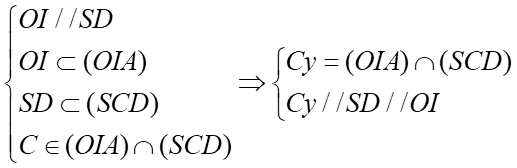 .
.
c) Sai. Tứ giác  là hình bình hành nên
là hình bình hành nên  .
.
Ta có: 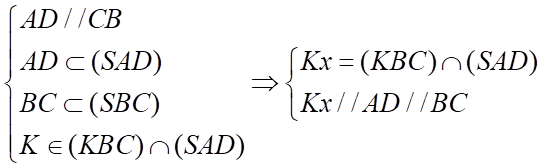 .
.
Trong 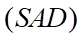 gọi
gọi 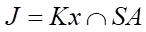 , có
, có 
d) Đúng. Ta có:
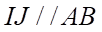 (
(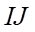 là đường trung bình của
là đường trung bình của 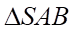 )
)
 .
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: 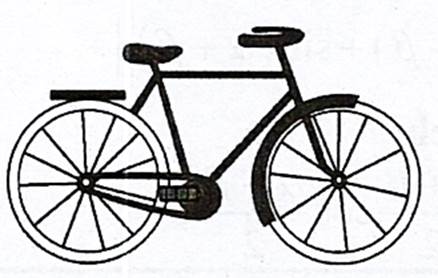 Một bánh xe đạp quay được 25 vòng trong 10 giây. Tính độ dài quãng đường mà người đi xe thực hiện được trong 2,35 phút, biết rằng bán kính bánh xe bằng
Một bánh xe đạp quay được 25 vòng trong 10 giây. Tính độ dài quãng đường mà người đi xe thực hiện được trong 2,35 phút, biết rằng bán kính bánh xe bằng 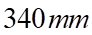 .
.
Lời giải
Trả lời: 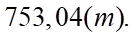
Sau 2,35 phút, số vòng mà bánh xe thực hiện được là:
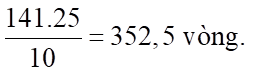 Bán kính bánh xe:
Bán kính bánh xe: 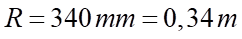 .
.
Quãng đường mà người đi xe đạp thực hiện được sau 2,35 phút là:

Câu 2: Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là 100 nghìn đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30 nghìn đồng so với giá của mét khoan ngay trước đó. Một người cần khoan một giếng sâu 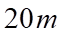 để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
Lời giải
Trả lời: 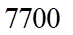 .
.
Gọi  là giá của mét khoan thứ
là giá của mét khoan thứ 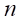 , trong đó
, trong đó 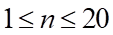 .
.
Khi đó,  là cấp số cộng có số hạng đầu
là cấp số cộng có số hạng đầu 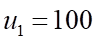 và công sai
và công sai 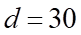 .
.
Số tiền mà gia đình phải thanh toán cho cơ sở khoan giếng là:
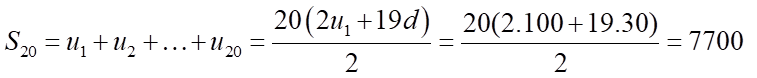 .
.
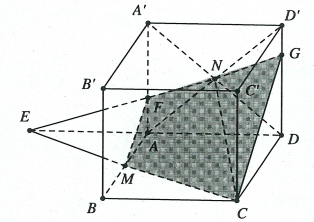
Câu 3: Cho hình lập phương 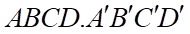 cạnh
cạnh 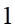 . Gọi
. Gọi 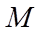 là trung điểm của
là trung điểm của 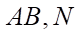 là tâm hình vuông
là tâm hình vuông 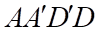 . Diện tích thiết diện của hình lập phương
. Diện tích thiết diện của hình lập phương 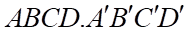 tạo bởi mặt phẳng
tạo bởi mặt phẳng 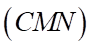 được viết dưới dạng
được viết dưới dạng 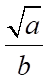 . Tính
. Tính 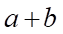 .
.
Lời giải
Trả lời: 18
Gọi 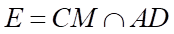 thì
thì 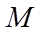 là trung điểm của
là trung điểm của 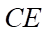 , nối
, nối 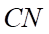 cắt
cắt 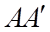 và
và 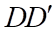 lần lượt tại các điểm
lần lượt tại các điểm 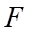 và
và 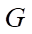 . Khi đó thiệt diện là tứ giác
. Khi đó thiệt diện là tứ giác 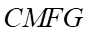 .
.
Do 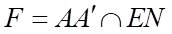 nên
nên 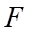 là trọng tâm tam giác
là trọng tâm tam giác 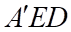 nên
nên 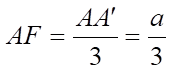
 Ta có:
Ta có: 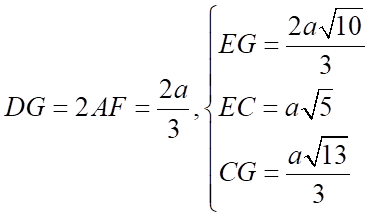
Lại có: 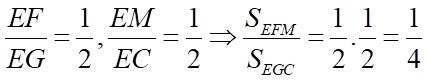 nên
nên 
Suy ra 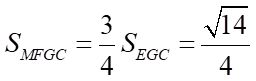 . Vậy
. Vậy 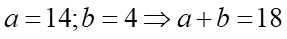 .
.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng và đường thẳng SC. Tỉ số 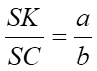 , tính
, tính 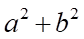 .
.
Lời giải
Trả lời: 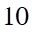
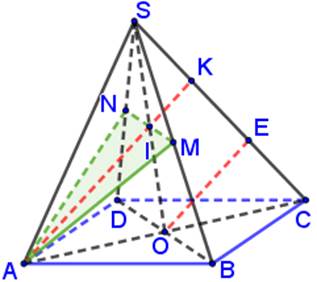
Gọi O = AC Ç BD, ta có OS Ç MN = I là trung điểm OS.
Gọi E là trung điểm KC thì OE là đường trung bình trong ΔACK. Suy ra OE // AK.
Với I là trung điểm OS thì IK là đường trung bình trong ΔOES. Vậy K là trung điểm ES.
Từ và suy ra SK = KE = EC hay 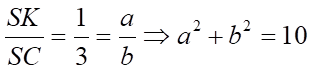 .
.
Câu 5: Một cái hồ chứa 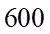 lít nước ngọt. Người ta bơm nước biển có nồng độ muối
lít nước ngọt. Người ta bơm nước biển có nồng độ muối 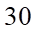 gam/lít vào hồ với tốc độ
gam/lít vào hồ với tốc độ 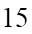 lít/phút. Hỏi nồng độ muối trong hồ sẽ thế nào khi
lít/phút. Hỏi nồng độ muối trong hồ sẽ thế nào khi 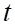 dần tới dương vô cùng?
dần tới dương vô cùng?
Lời giải
Trả lời: 30
Sau 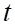 phút bơm nước vào hồ thì lượng nước là
phút bơm nước vào hồ thì lượng nước là 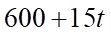
Sau 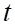 phút bơm lượng muối có được là
phút bơm lượng muối có được là 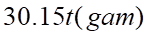 .
.
Nồng độ muối của nước là: 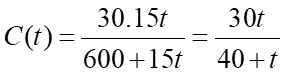 gam/lít.
gam/lít.
Khi 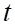 dần về dương vô cùng, ta có:
dần về dương vô cùng, ta có:
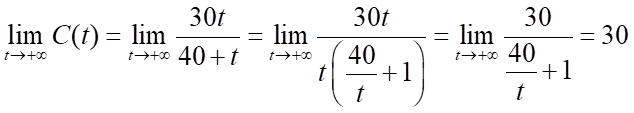 gam/lít.
gam/lít.
Câu 6: Cho hàm số 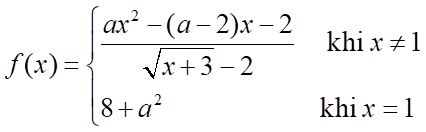 . Có tất cả bao nhiêu giá trị của
. Có tất cả bao nhiêu giá trị của 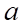 để
để
hàm số liên tục tại 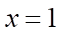 ?
?
Lời giải
Trả lời: 2.
Tập xác định: 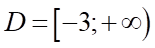 .
.
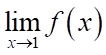
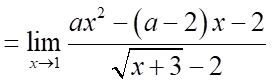 .
.
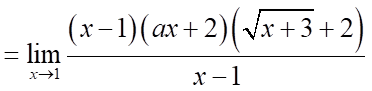 .
.
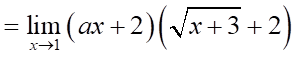
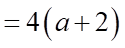 .
.
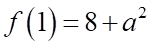 .
.
Hàm số đã cho liên tục tại 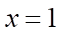 khi
khi 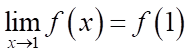
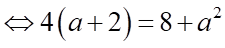
 .
.
Vậy có 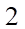 giá trị của
giá trị của 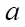 để hàm số đã cho liên tục tại
để hàm số đã cho liên tục tại 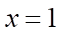 .
.
-------------- Hết --------------







Bạn cần đặt mua gói tài liệu này để xem bình luận