Lythuyetbai11check
CHƯƠNG IV: NGUYÊN HÀM VÀ TÍCH PHÂN
BÀI 11. NGUYÊN HÀM
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. NGUYÊN HÀM CỦA 1 HÀM SỐ
Cho hàm số ![]() xác định trên một
khoảng
xác định trên một
khoảng ![]() (hoặc một
đoạn, hoặc một nửa khoảng). Hàm số
(hoặc một
đoạn, hoặc một nửa khoảng). Hàm số ![]() được gọi
là một nguyên hàm của hàm số
được gọi
là một nguyên hàm của hàm số ![]() trên
trên
![]() nếu
nếu ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() .
.
Chú ý. Trường hợp ![]() thì các đẳng thức
thì các đẳng thức
![]() và
và ![]() được hiểu
là đạo hàm bên phải tại điểm
được hiểu
là đạo hàm bên phải tại điểm ![]() và đạo hàm bên
trái tại điểm
và đạo hàm bên
trái tại điểm ![]() của
hàm số
của
hàm số ![]() , tức là
, tức là
![]()
Ví dụ 1. Cho hàm số ![]() .
Trong các hàm số cho dưới đây, hàm số nào là một
nguyên hàm của hàm số
.
Trong các hàm số cho dưới đây, hàm số nào là một
nguyên hàm của hàm số ![]() trên
trên ![]() ?
?
a) ![]() ; b)
; b)
![]() .
.
Ta có: ![]() .
.
Vì ![]() với mọi
với mọi ![]() nên hàm số
nên hàm số ![]() là một nguyên hàm của
là một nguyên hàm của
![]() trên
trên ![]() .
.
Hàm số ![]() không là nguyên hàm của
không là nguyên hàm của
![]() trên
trên ![]() vì với
vì với ![]() , ta có
, ta có![]()
Định nghĩa
Giả sử hàm số
![]() là một nguyên hàm của
là một nguyên hàm của
![]() trên
trên ![]() . Khi đó:
. Khi đó:
a) Với mỗi hằng
số ![]() , hàm số
, hàm số ![]() cũng là một
nguyên hàm của
cũng là một
nguyên hàm của ![]() trên
trên ![]() ;
;
b) Nếu hàm số
![]() là một nguyên hàm của
là một nguyên hàm của
![]() trên
trên ![]() thì tồn tại một
hằng số
thì tồn tại một
hằng số ![]() sao cho
sao cho ![]() với mọi
với mọi ![]() .
.
Như vậy, nếu
![]() là một nguyên hàm của
là một nguyên hàm của
![]() trên
trên ![]() thì mọi nguyên hàm của
thì mọi nguyên hàm của
![]() trên
trên ![]() đều có dạng
đều có dạng
![]() (
(![]() là hằng số). Ta
gọi
là hằng số). Ta
gọi ![]() là họ các nguyên hàm của
là họ các nguyên hàm của
![]() trên
trên ![]() , kí hiệu bởi
, kí hiệu bởi ![]() .
.
Chú ý:
a) Để tìm họ
các nguyên hàm (gọi tắt là tìm nguyên hàm) của hàm số ![]() trên
trên ![]() , ta chỉ cần tim
một nguyên hàm
, ta chỉ cần tim
một nguyên hàm ![]() của
của ![]() trên
trên ![]() và khi đó
và khi đó![]() là hằng số.
là hằng số.
b) Người ta chứng
minh được rằng, nếu hàm số ![]() liên tục trên khoảng
liên tục trên khoảng
![]() thì
thì ![]() có nguyên hàm trên khoảng
đó.
có nguyên hàm trên khoảng
đó.
c) Biểu thức ![]() gọi là vi phân của
nguyên hàm
gọi là vi phân của
nguyên hàm ![]() , kí hiệu là
, kí hiệu là ![]() . Vậy
. Vậy ![]() .
.
d) Khi tìm nguyên hàm của
một hàm số mà không chỉ rõ tập ![]() , ta hiểu là tìm nguyên
hàm của hàm số đó trên tập xác định
, ta hiểu là tìm nguyên
hàm của hàm số đó trên tập xác định
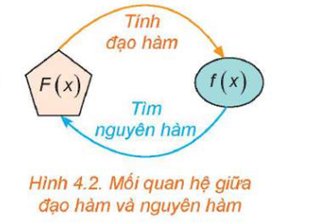
Ví dụ 2. Tìm một nguyên hàm của hàm số ![]() trên
trên ![]() . Từ đó hãy tìm
. Từ đó hãy tìm ![]() .
.
Lời giải
Vì 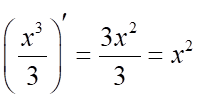 nên
nên ![]() là một nguyên hàm của
hàm số
là một nguyên hàm của
hàm số ![]() trên
trên ![]() . Do đó,
. Do đó, ![]() .
.
2. TÍNH CHẤT CƠ BẢN CỦA NGUYÊN HÀM
Nguyên hàm của tích một hàm số với một hằng số khác 0
![]()
Ví dụ 3. Sử dụng kết quả của Ví dụ 2, hãy tìm:
a) ![]() b)
b)
![]()
Lời giải
Ta có:
a) ![]() .
.
b) ![]() .
.
Nguyên hàm của một tổng
![]()
![]()
Ví dụ 4. Sử dụng kết quả của Luyện tập 3 và tính chất cơ bản của nguyên hàm, hãy tìm:
a) ![]() ; b)
; b)
![]() .
.
Lời giải
Ta có:
a) ![]() .
.
b) ![]()
Ví dụ 5. Giải bài toán : Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận
tốc của máy
bay khi chạy đà được cho bởi ![]() , với
, với ![]() là thời gian (tính bằng
giây) kể từ khi máy bay bắt đầu chạy
đà. Sau 30 giây thì máy bay cất cánh rời đường
băng. Quãng đường máy bay đã di chuyển từ
khi bắt đầu chạy đà đến khi rời
đường băng là bao nhiêu mét?
là thời gian (tính bằng
giây) kể từ khi máy bay bắt đầu chạy
đà. Sau 30 giây thì máy bay cất cánh rời đường
băng. Quãng đường máy bay đã di chuyển từ
khi bắt đầu chạy đà đến khi rời
đường băng là bao nhiêu mét?
Lời giải
Gọi ![]() là quãng đường
máy bay di chuyển được sau
là quãng đường
máy bay di chuyển được sau ![]() giây
kể từ lúc bắt đầu chạy đà.
giây
kể từ lúc bắt đầu chạy đà.
Ta có ![]() . Do đó,
. Do đó, ![]() là một nguyên hàm của
hàm số vận tốc
là một nguyên hàm của
hàm số vận tốc ![]() . Sử
dụng tính chất của nguyên hàm ta được
. Sử
dụng tính chất của nguyên hàm ta được![]() Theo giả thiết,
Theo giả thiết, ![]() nên
nên ![]() và ta được
và ta được ![]() .
.
Máy bay rời
đường băng khi ![]() (giây)
nên
(giây)
nên ![]() .
.
Vậy quãng
đường máy bay đã di chuyển từ khi bắt
đầu chạy đà đến khi nó rời đường
băng là ![]() .
.
3. NGUYÊN HÀM CỦA MỘT SỐ HÀM SỐ THƯỜNG GẶP
a) Nguyên hàm của hàm số lũy thừa
Hàm số luỹ thừa
![]() có đạo hàm với
mọi
có đạo hàm với
mọi ![]() và
và![]()
![]() .
. ![]() .
.
Ví dụ 6. Tìm:
a) ![]() ; b)
; b) ![]() ; c)
; c)
![]() .
.
Lời giải
a) 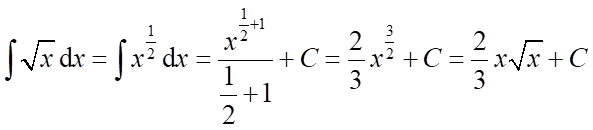 .
.
b) ![]() .
.
c) ![]() .
.
b) Nguyên hàm của hàm số lượng giác
![]()
![]()
![]()
![]()
Ví dụ 7. Tìm:
a) ![]() b)
b)
![]()
Lời giải
a) ![]() .
.
b) ![]() .
.
c) Nguyên hàm của hàm số mũ
![]()
![]()
Ví dụ 8. Tìm:
a) ![]() ; b)
; b)
![]() ; c)
; c)
![]() .
.
Lời giải
a) ![]() .
.
b) 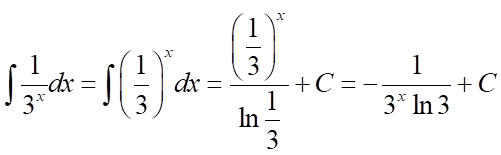 .
.
c) ![]() .
.
Ta tổng kết lại bảng nguyên hàm của một số hàm số thường gặp như sau.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dựa vào bảng nguyên hàm của các hàm số thường gặp và tính chất cơ bản của nguyên hàm, ta có thể tìm được nguyên hàm của nhiều hàm số khác.
B. GIẢI BÀI TẬP SÁCH GIÁO KHOA
4.1. Trong mỗi trường hợp sau, hàm số
![]() có là một nguyên hàm
của hàm số
có là một nguyên hàm
của hàm số ![]() trên khoảng
tương ứng không? Vì sao?
trên khoảng
tương ứng không? Vì sao?
a) ![]() và
và ![]() trên khoảng
trên khoảng ![]() ;
;
b) ![]() và
và ![]() trên
trên ![]() .
.
Lời giải
a) Có ![]() .
.
Do đó, hàm số ![]() là một nguyên hàm của
hàm số
là một nguyên hàm của
hàm số ![]() trên khoảng
trên khoảng ![]() .
.
b) Có ![]() .
.
Do đó, hàm số ![]() không là nguyên hàm của
hàm số
không là nguyên hàm của
hàm số ![]() trên
trên ![]() .
.
4.2. Tìm nguyên hàm của các hàm số sau:
a) ![]() b)
b)
![]()
c) ![]() ; d)
; d)
![]() .
.
Lời giải
a) ![]()
b) ![]()
c) ![]()
![]()
d)![]()
![]()
4.3. Tìm:
a) ![]() b)
b)
![]() ;
;
c) ![]() ; d)
; d)
![]() .
.
Lời giải
a) ![]()
![]()
b) ![]()
![]()
c) ![]()
![]()
d) ![]()
4.4. Tìm:
a) ![]() ; b)
; b)
![]() ;
;
c) ![]() d)
d)
![]()
Lời giải
a) ![]()
b) ![]()
c) ![]()
![]()
d) ![]()
![]()
4.5. Cho hàm số ![]() xác
định trên khoảng
xác
định trên khoảng ![]() . Biết
rằng,
. Biết
rằng, ![]() với mọi
với mọi
![]() và
và ![]() . Tính giá trị
. Tính giá trị ![]() .
.
Lời giải
Vì ![]() nên
nên![]()
Mà ![]() nên
nên ![]() , suy ra
, suy ra ![]() . Do đó, hàm số
. Do đó, hàm số ![]()
Vậy ![]()
4.6. Cho hàm số ![]() có
đồ thị là
có
đồ thị là ![]() . Xét
điểm
. Xét
điểm ![]() thay đổi
trên
thay đổi
trên ![]() . Biết rằng, hệ
số góc của tiếp tuyến của đồ thị
. Biết rằng, hệ
số góc của tiếp tuyến của đồ thị
![]() tại
tại ![]() là
là ![]() và điểm
và điểm ![]() trùng với gốc
toạ độ khi nó nằm trên trục tung. Tìm biểu
thức
trùng với gốc
toạ độ khi nó nằm trên trục tung. Tìm biểu
thức ![]() .
.
Lời giải
Vì hệ số góc
của tiếp tuyến của đồ thị ![]() tại
tại ![]() là
là ![]() nên ta có:
nên ta có:
![]()
![]()
Vì điểm M
trùng với gốc tọa độ khi nó nằm trên trục
tung nên ![]() .
.
Do đó ![]()
Do đó ![]()
4.7. Một viên đạn được bắn
thẳng đứng lên trên từ mặt đất. Giả
sử tại thời điểm ![]() giây
(coi
giây
(coi ![]() là thời điểm
viên đạn được bắn lên), vận tốc của
nó được cho bởi
là thời điểm
viên đạn được bắn lên), vận tốc của
nó được cho bởi ![]() .
Tìm độ cao của viên đạn (tính từ mặt
đất):
.
Tìm độ cao của viên đạn (tính từ mặt
đất):
a) Sau ![]() giây;
giây;
b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất).
Lời giải
Gọi ![]() là độ cao của
viên đạn bắn lên từ mặt đất sau
là độ cao của
viên đạn bắn lên từ mặt đất sau ![]() giây kể từ thời
điểm đạn được bắn lên.
giây kể từ thời
điểm đạn được bắn lên.
Khi đó ![]() . Vì S(0)
. Vì S(0) ![]() nên
nên ![]() .
.
Do đó ![]() .
.
a) Sau 5 giây độ
cao của viên đạn là: ![]() .
.
b) Có ![]()
![]()
![]()
Viên đạn
đạt độ cao lớn nhất là ![]() khi
khi ![]() giây.
giây.
C. CÁC DẠNG TOÁN
1. Phương pháp
Dùng các phép biến
đổi, các phương pháp tính nguyên hàm đưa nguyên
hàm về nguyên hàm hàm đa thức: ![]() ;
;
![]()
2. Ví dụ
Ví dụ 1. Tính ![]()
Lời giải
Ta có ![]() .
.
Ví dụ 2. Tìm họ tất cả
nguyên hàm của hàm số ![]()
Lời giải
Ta có ![]() .
.
Ví dụ 3. Tìm họ
nguyên hàm của hàm số ![]()
Lời giải
![]()
![]() .
.
Ví dụ 4: Tìm nguyên hàm của hàm số ![]() .
.
Lời giải
Ta có: ![]()
![]() .
.
Khi đó: ![]()
![]() =
=![]() .
.
Ví dụ 5:
Biết hàm số ![]() có
có
![]() ,
,![]() và
đồ thị của hàm số
và
đồ thị của hàm số ![]() cắt
trục tung tại điểm có tung độ bằng
cắt
trục tung tại điểm có tung độ bằng ![]() .
Tìm hàm số
.
Tìm hàm số ![]()
Lời giải
Theo lý thuyết ta có:![]() .
.
Ta có: ![]()
![]() .
.
Khi đó ![]() có
dạng:
có
dạng: ![]()
Theo đề ta có: 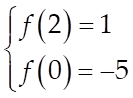
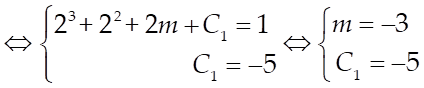 .
.
Vậy hàm số ![]() .
.
1. Phương pháp: Tách hàm số muốn lấy nguyên hàm thành các hàm số phân thức cơ bản:
![]()
![]()
![]()
![]() ;
;
![]()
![]()
2. Các ví dụ
Ví dụ 1: Cho ![]() là
một nguyên hàm của hàm số
là
một nguyên hàm của hàm số ![]() ; biết
; biết ![]() . Tính
. Tính ![]() .
.
Lời giải
Ta có ![]() ;
;
![]()
![]()
![]() .
.
Ví dụ 2: Tính nguyên hàm ![]() .
.
Lời giải
Ta có: ![]()
![]()
![]() .
.
Ví dụ 3:
Tìm nguyên hàm ![]()
Lời giải
![]()
Ví dụ 4:
Biết ![]() là một nguyên
hàm của hàm số
là một nguyên
hàm của hàm số ![]() và
và
![]() Tính
Tính ![]()
Lời giải
![]()
Do ![]() nên
nên ![]()
Ví dụ 5: Biết
![]() Tính giá trị biểu
thức
Tính giá trị biểu
thức ![]()
Lời giải
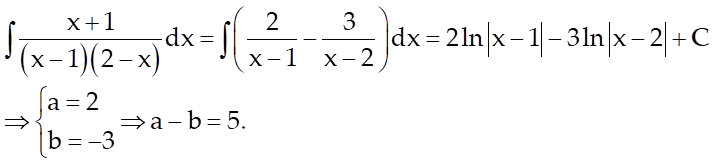
1. Phương pháp
Đổi biến số đưa nguyên hàm cần tìm về nguyên hàm của hàm lũy thừa hoặc nguyên hàm của hàm phân thức.
Chú ý thêm các công thức mở rộng sau:
|
|
|
|
|
|
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1:
Tìm nguyên hàm của hàm số ![]()
Lời giải
![]()
Ví dụ 2: Tìm
nguyên hàm ![]()
Lời giải
Ta có 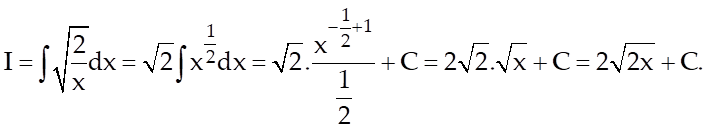
Ví dụ 3:
Tính ![]()
Lời giải
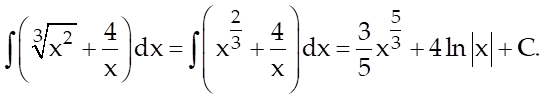
Dạng 4. Nguyên hàm của hàm số lượng giác
1. Phương pháp
* Bảng nguyên hàm cơ bản:
![]()
![]()
![]()
![]()
![]()
![]()
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1:
Tìm nguyên hàm của hàm số ![]()
Lời giải
Ta có: ![]()
Ví dụ 2:
Tìm nguyên hàm ![]()
Lời giải
Ta có ![]()
Ví dụ 3:
Tìm nguyên hàm của hàm số ![]()
Lời giải
Ta có ![]()
Suy ra ![]()
Ví dụ 4: Cho
![]() và
và ![]() Tính
Tính ![]()
Lời giải
Ta có: ![]()
![]()
![]()
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho ![]() . Tìm
. Tìm ![]()
Lời giải
Ta có ![]()
![]()
![]() .
.
Vậy ![]()
![]()
![]() .
.
Ví dụ 2:
Hàm số ![]() có một nguyên hàm là
có một nguyên hàm là ![]() .
Tìm nguyên hàm của hàm số
.
Tìm nguyên hàm của hàm số ![]()
Lời giải
Ta có: ![]()
Suy ra: ![]() .
.
Ví dụ 3:
Cho ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() thỏa
mãn
thỏa
mãn ![]() .
Tìm
.
Tìm ![]()
Lời giải
Cách 1: Xét đáp án ![]() ,
ta có:
,
ta có: 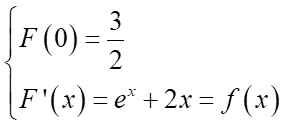 .
.
Cách 2: Ta có ![]() .
.
![]() là 1 nguyên hàm của hàm số
là 1 nguyên hàm của hàm số ![]() suy
ra
suy
ra ![]() có
dạng
có
dạng ![]()
Theo đề bài ![]() Vậy
Vậy
![]()
Ví dụ 4. Biết
![]() là một nguyên hàm của
hàm số
là một nguyên hàm của
hàm số ![]() và
và ![]() . Tính
. Tính ![]()
Lời giải
![]() .
.
Khi đó ![]() .
.
Dạng 6: Bài tập tổng hợp
Câu 1: Cho hàm số![]() , ta có
, ta có ![]() . Giá trị của biểu
thức
. Giá trị của biểu
thức ![]() bằng
bằng
Lời giải
Vì![]() nên
nên![]()
Suy ra ![]() đồng
nhất 2 biểu thức ta được hệ
phương trình sau:
đồng
nhất 2 biểu thức ta được hệ
phương trình sau: 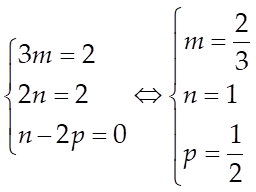 . Suy ra:
. Suy ra: ![]() .
.
Câu 2: Gọi ![]() là
một nguyên hàm của hàm số
là
một nguyên hàm của hàm số ![]() , thỏa mãn
, thỏa mãn ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() .
.
Lời giải
Ta có ![]()
![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() ,
ta có
,
ta có ![]() mà
mà ![]()
![]() .
.
![]()
![]()
![]()
![]()
Câu 3: Cho hàm số ![]() xác định trên
xác định trên ![]() thỏa
mãn
thỏa
mãn ![]() ,
, ![]() ,
, ![]() .
Tính
.
Tính ![]() .
.
Lời giải
Trên khoảng ![]() :
: ![]()
![]()
![]() .
.
Mà ![]() .
.
Trên khoảng ![]()
![]()
![]()
![]() .
.
Mà ![]()
![]() .
.
Vậy 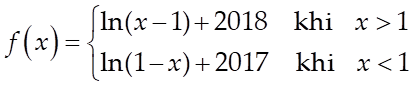 .
Suy ra
.
Suy ra ![]() .
.
Câu 4: Biết ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên
trên
![]() . Tính
. Tính![]()
Lời giải
Tính ![]()
![]() .
.
Suy ra 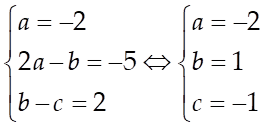 nên
nên
![]() .
.
Tính ![]() suy
ra
suy
ra ![]() .
.
Câu 5: Cho hàm số ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() với mọi
với mọi ![]() . Tính
. Tính ![]() .
.
Lời giải
Ta có: ![]()
![]() .
.
Với ![]() thì
thì
![]() .
.
Do đó ![]() .
Vậy
.
Vậy ![]() hay
hay ![]() .
.
Câu 6: Cho hàm số ![]() xác
định trên
xác
định trên ![]() , thỏa mãn
, thỏa mãn ![]() ,
, ![]() và
và ![]() . Tính
. Tính ![]() biết rằng
biết rằng ![]() .
.
Lời giải
Vì ![]() , nên ta có:
, nên ta có: ![]()
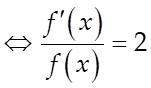
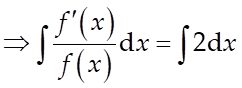 .
.
![]()
![]()
![]() .
.
Cho ![]()
![]()
![]()
![]()
Do đó: ![]()
![]()
![]() . Do đó:
. Do đó:![]() .
.
Câu 7: Cho hàm số ![]() thỏa
mãn
thỏa
mãn ![]() và
và ![]()
![]()
![]() . Tính giá trị của
. Tính giá trị của ![]()
Lời giải
Ta có ![]()
![]()
Lại có ![]() nên
nên ![]() do đó
do đó ![]()
![]()
![]()
Mà ![]() nên
nên ![]() . Vậy
. Vậy![]()
Câu 8: Cho hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() thỏa mãn
thỏa mãn 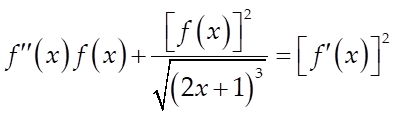 và
và ![]() với mọi
với mọi ![]() . Biết rằng
. Biết rằng ![]() .
Tính giá trị của
.
Tính giá trị của ![]()
Lời giải
Ta có: 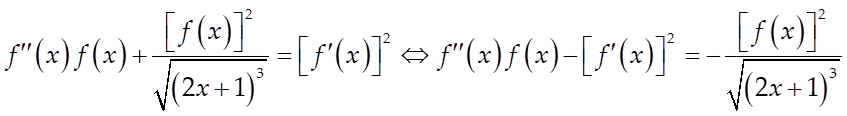
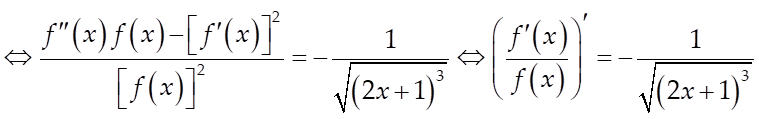
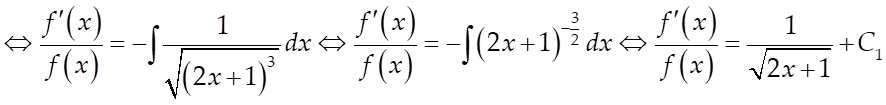 .
.
Thay ![]() ta
được:
ta
được: ![]() .
.
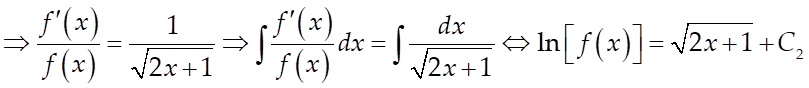
Thay ![]() ta được
ta được![]() .
.![]()
Thay ![]() ta được
ta được ![]() .
.
Dạng 7 : Toán thực tế
Ví dụ 1.
Khi được thả từ độ cao 20 m, một vật
rơi với gia tốc không đổi ![]() . Sau khi rơi
đ̛ược
. Sau khi rơi
đ̛ược ![]() giây thì
vật có tốc độ bao nhiêu và đi được
quãng đường bao nhiêu?
giây thì
vật có tốc độ bao nhiêu và đi được
quãng đường bao nhiêu?
Lời giải
Kí hiệu ![]() là tốc độ
của vật,
là tốc độ
của vật, ![]() là quãng
đường vật đi được cho đến
thời điểm
là quãng
đường vật đi được cho đến
thời điểm ![]() giây kể
từ khi vật bắt đầu rơi. Vì
giây kể
từ khi vật bắt đầu rơi. Vì ![]() với mọi
với mọi ![]() nên
nên ![]() Ta có
Ta có ![]() nên
nên ![]() hay
hay ![]() . Vậy
. Vậy ![]() .
.
Vì ![]() với mọi
với mọi ![]() nên
nên ![]() Ta có
Ta có ![]() nên
nên ![]() hay
hay ![]() . Vậy
. Vậy ![]() . Vật rơi từ
độ cao 20 m nên
. Vật rơi từ
độ cao 20 m nên ![]() , suy ra
, suy ra ![]() . Vậy sau khi vật
rơi được
. Vậy sau khi vật
rơi được ![]() giây
giây ![]() thì vật có tốc
độ
thì vật có tốc
độ ![]() và đi
được quãng đường
và đi
được quãng đường ![]() .
.
Ví dụ 2.
Kí hiệu ![]() là chiều
cao của một cây (tính theo mét) sau khi trồng
là chiều
cao của một cây (tính theo mét) sau khi trồng ![]() năm. Biết rằng
sau năm đầu tiên cây cao 2 m . Trong 10 năm tiếp
theo, cây phát triển với tốc độ
năm. Biết rằng
sau năm đầu tiên cây cao 2 m . Trong 10 năm tiếp
theo, cây phát triển với tốc độ ![]() (m/ năm).
(m/ năm).
a) Xác định
chiều cao của cây sau ![]() năm
năm
![]() .
.
b) Sau bao nhiêu năm cây cao 3 m ?
Lời giải
a) Chiều cao của
cây sau ![]() năm là:
năm là: ![]() .
.
Mà ![]() nên
nên ![]() . Do đó
. Do đó ![]() .
.
b) Cây cao ![]() tức là
tức là ![]() . Vậy sau khoảng
2,72 năm thì cây cao
. Vậy sau khoảng
2,72 năm thì cây cao ![]() .
.
Ví dụ 3.
Một chiếc xe đang chuyển động với tốc
độ ![]() thì tăng tốc
với gia tốc không đổi
thì tăng tốc
với gia tốc không đổi ![]() .
Tính quãng đường xe đó đi được trong
3 giây kể từ khi bắt đầu tăng tốc.
.
Tính quãng đường xe đó đi được trong
3 giây kể từ khi bắt đầu tăng tốc.
Lời giải
Kí hiệu ![]() là tốc
độ của xe,
là tốc
độ của xe, ![]() là quãng
đường xe đi được cho đến
thời điểm
là quãng
đường xe đi được cho đến
thời điểm ![]() giây kể từ khi xe tăng tốc.
giây kể từ khi xe tăng tốc.
Vì ![]() nên
nên ![]() . Mà
. Mà ![]() nên
nên ![]() . Do đó
. Do đó ![]() .
.
Có ![]() . Vì
. Vì ![]() . Do đó
. Do đó ![]() . Quãng đường xe đó đi được
trong 3 giây kể từ khi bắt đầu tăng tốc
là
. Quãng đường xe đó đi được
trong 3 giây kể từ khi bắt đầu tăng tốc
là ![]()
Ví dụ 4: Vi khuẩn HP (Helicobacter pylori)
gây đau dạ dày tại ngày thứ t với số
lượng là F(t), biết nếu phát hiện sớm
khi số lượng vi khuẩn không vượt quá 5000 con
thì bệnh nhân sẽ được cứu chữa. Biết
tốc độ phát triển của vi khuẩn tại
ngày thứ t là ![]() và ban
đầu bệnh nhân có 2000 con vi khuẩn. Sau 10 ngày bệnh
nhân phát hiện ra bị bệnh. Hỏi khi đó có bao nhiêu
con vi khuẩn trong dạ dày ( lấy xấp xỉ hàng thập
phân thứ hai)?
và ban
đầu bệnh nhân có 2000 con vi khuẩn. Sau 10 ngày bệnh
nhân phát hiện ra bị bệnh. Hỏi khi đó có bao nhiêu
con vi khuẩn trong dạ dày ( lấy xấp xỉ hàng thập
phân thứ hai)?
Lời giải
Tốc độ phát triển của
vi khuẩn tại ngày thứ t là ![]() .
Suy ra số lượng vi khuẩn vào ngày thứ t
được tính theo công thức
.
Suy ra số lượng vi khuẩn vào ngày thứ t
được tính theo công thức
![]() .
.
Lúc ban đầu bệnh nhân có 2000 con vi khuẩn nên
![]()
![]() .
.
Số
vi khuẩn sau 10 ngày là ![]() con
con
Ví dụ 5: Tốc độ thay đổi
số dân của một thị trấn kể từ
năm 1970 được mô tả bằng công thức 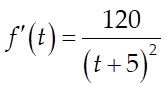 , với t là thời
gian tính bằng năm (thời điểm t = 0 ứng
với năm 1970). Biết rằng số dân của thị
trấn vào năm 1970 là 2000 người. Hỏi số dân của
thị trấn đó vào năm 2008 ước tính là bao nhiêu
?
, với t là thời
gian tính bằng năm (thời điểm t = 0 ứng
với năm 1970). Biết rằng số dân của thị
trấn vào năm 1970 là 2000 người. Hỏi số dân của
thị trấn đó vào năm 2008 ước tính là bao nhiêu
?
Lời giải
Tốc độ thay
đổi số dân của thị trấn vào năm thứ
t là ![]() . Suy ra nguyên
hàm của
. Suy ra nguyên
hàm của ![]() là hàm số
là hàm số ![]() mô tả số dân của
thị trấn vào năm thứ t. Ta có
mô tả số dân của
thị trấn vào năm thứ t. Ta có
![]() .
.
Số dân của thị trấn vào năm 1970 (ứng với t = 0) là
![]()
![]() .
.
Vậy số dân của thị trấn vào năm 2008 (ứng với t = 38) là
![]() ngàn
người.
ngàn
người.







Bạn cần đặt mua gói tài liệu này để xem bình luận